The Competence Trap (and Why it Keeps You From Trying New Things)

A reader asked me recently whether I thought there was a limit to how much math you could learn, based on your intelligence. As in, if your IQ was too low you’d get stuck at algebra or calculus and be unable to learn any more math.

This seems highly unlikely. The way deep subjects like math are learned is through a process of increasingly abstract chunking of simpler mathematical ideas. It would be really strange if this process just dead-ended at some arbitrary point.

Another observation that easily refutes this point is simply how much more mathematical everybody is than in ages past. Counting beyond the number four is undeveloped in some cultures. Before mass education, most people were innumerate. As my friend, Kalid Azad, likes to point out—rewind time far enough and things like the concept of “zero” were PhD-level insights!

So if the existence of a mathematical barrier that prevents less-clever people from going forward is unlikely. Yet why does it often feel that way? Maybe you were pretty good at math in elementary school, but gradually it seemed to get harder and more painful.

Differences in Learning Rate

While I doubt there’s an intrinsic barrier arbitrarily up the abstraction continuum for mathematics, it’s likely that people differ in mathematical aptitude. The average IQ for professional physicists is north of 150—putting them in the top .2%.

A more reasonable explanation might be that it takes some people longer to form the relevant building-block insights to progress through math. If it took you only a month to “get” calculus, you will move faster and further than someone who needed an entire year. This insight-acquiring process may vary from person-to-person, in the same way that things like working memory or visuospatial skills are known to vary.

This suggests the obstacle to learning a lot of math is intellectual. There’s no barrier per se, but the obstacle to learning advanced mathematics is that it may take you longer than someone who is very clever.

But there is another explanation…

Is the Learning Barrier Affective or Cognitive?

Both the idea of an arbitrary barrier or variation in learning speed are cognitive challenges. Cognitive, in this sense, means the process of thinking, understanding and remembering. It would suggest that we’re all the same, just some people have an easier time.

There’s no doubt that cognitive differences are a partial explanation. But I’d argue that the affective part—meaning our motivation, moods and interest—plays at least as large a role in how difficult it is to keep learning math.

Keep in mind the point made earlier. Hundreds of years ago knowing any math was a sign you were very smart. If you understood negative numbers in the 1300s, that would have been as rare as understanding string theory today.

As standards have risen, what it means to understand negative numbers has changed dramatically. It would have been a mindblowing insight to a medieval peasant, but now it’s just a mandatory part of your 6th-grade math class.

The Competence Trap

In contrast to being a cognitive barrier, I think the more important explanation is a motivational barrier.

Self-determination theory argues that autonomy, competence and relatedness are basic psychological needs. Any behaviors that worsen these needs are going to be demotivating. So even if you had a natural interest in math, if you feel like you’re no good at it (competence), that doing poorly will result in others thinking less of you (relatedness) or you feel forced to do it for school (autonomy), it’s unsurprising that motivation plummets.

In contrast, if you felt like you were pretty good at math you might get reinforcement from the teacher and peers (relatedness), feelings of skill as you take on new challenges (competence), and you might even seek out to understand things yourself (autonomy). Your interest in math grows, just as it withers for the people who weren’t as lucky.

I’m using math as an example, but it applies to anything: sports, music, athletics, languages, socializing or art. Motivation amplifies small differences.

Play and Opportunity Cost

We don’t just compare ourselves to others, but within ourselves. The person who is objectively good at both math and languages, but somewhat better at math sees herself as a “math person.” This may lead to extra investments of time in math classes, reinforcing her strengths.

One outcome of this suggests that, as we get more skilled in some domains, we become (relatively) worse at everything else we haven’t yet mastered.

If we see our engagement in professions and hobbies as a way of getting rewards (money, respect, achievement or just fun) for the time we invest, we can see how this can create a trap. As you get better at some things, the opportunity cost to learn something else increases. This funnels you into a narrower set of hobbies, passions and work than you might otherwise be capable of.

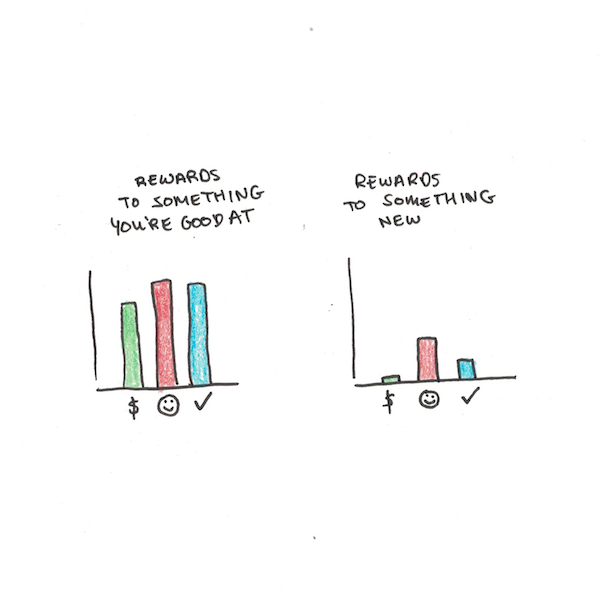
Is the Narrowing of Interests a Bad Thing?

Maybe this isn’t a problem. Our modern society is built off of specialization. Albert Einstein wouldn’t have come up with general relativity if he had needed to grow his own food and sew his own clothes. There just wouldn’t have been time to reach the depths of thinking required.

Similarly, if you enjoy painting, but not basketball, there isn’t a problem if you choose to spend your time with a brush rather than on the court. Most of us don’t need advanced math, so the fact that many of us lose interest in it is probably functional. We know we won’t be mathematicians so we use our limited time to focus on something we can be good at.

I enjoy learning lots of different things. I think it tends to be more satisfying and interesting than narrow specialization. But perhaps this is also my motivational reinforcement showing, as I’ve also been able to meet my psychological needs doing so. I learn a lot because I like doing it. If I hated it, I’m not sure I could persist, even understanding the above point.

One flaw of a positive feedback loop, is that it tends to exaggerate small differences. Have a really discouraging math teacher may push you off the path to learning more math permanently.

Thus, I think our interests are artificially narrower than they could be. We could have more interesting hobbies, more diverse skills and more varied professional lives. True, some of the obstacles we face are cognitive—our talents lie elsewhere and so we build on our strengths—but much of the obstacles seem to be affective as well. We stay inside our boxes, not because we can’t climb out, but because we lose the curiosity to see what’s outside.