What is Understanding?

We all have an intuition about what it means to understand something. We all know what it’s like to be confused. We know both the pain of memorizing an answer you don’t understand as well as the satisfaction that comes from finally “getting it.” Yet what that intuition points to is hard to pin down.

The impetus to really understand what we’re learning was a central theme in my early writing. While I still agree this is important, I’m less clear what it means. Beyond this satisfying feeling, what does it mean to understand?

Some Understandings of Understanding

To sort out this confusion, let’s look at a few possibilities of what understanding might be.

1. Understanding as Connected Information

My original model of understanding was connected information: To understand something means having many connections between it and related ideas. Analogies assist with understanding by grafting a previous intuition onto a less familiar domain.

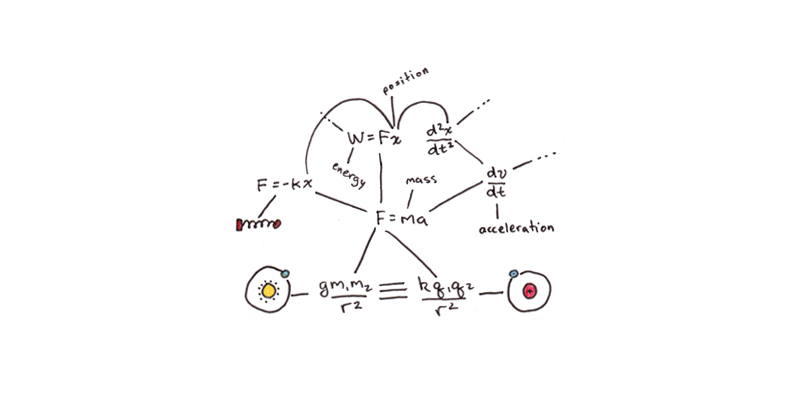
In this view, the key to developing understanding is to draw relationships between what you already understand and what you are trying to understand. Analogies, metaphors, visualizations, and associations try to find a fit between new and old knowledge.

This model is a useful starting point, but I think it has some flaws. A major one is simply a bootstrapping problem: If you don’t have some preliminary understanding, it’s very difficult to generate correct analogies.

This bootstrapping problem also suggests a different kind of “direct” understanding of something that precedes attempts to relate it to something else. We can understand many things without intermediating analogies, so it’s also possible that while connection-forming is a useful strategy, it may not fully describe what understanding actually is.

2. Understanding as Flexible Action

A different way of looking at understanding is application: To understand something means to be able to interact with it flexibly. The person who can deal with a wide range of algebra problems “understands” algebra in a way that a person who can only solve stereotyped formulas does not. Understanding physics means being able to deal with novel physics problems. Understanding chess means being able to play well from a variety of different positions.

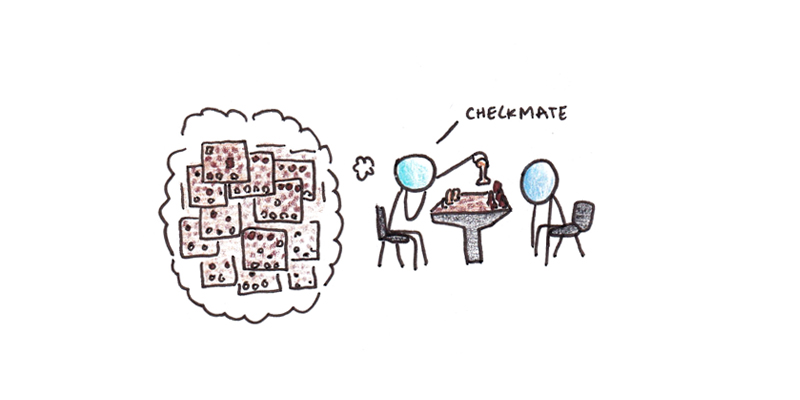
This perspective is bolstered by work in psychology that shows expertise resulting from a greater quantity of stored patterns. De Groot’s work with chess grandmasters found that the strongest players didn’t think further ahead than weaker players.¹ Instead, experts seem to rely on having many examples in memory to infer the correct move. The difference between useful understanding and rote memorization may have more to do with the sheer quantity of remembered patterns rather than a qualitative difference in the patterns themselves.

There’s probably truth to this perspective as well, but I suspect it’s incomplete. It doesn’t capture the feeling of insight when a concept “clicks” into place.

3. Understanding as Explanatory Ability

Flexible action may remove cases of rote memorization, but there are many situations where we can behave flexibly, but wouldn’t claim deep understanding.

I tried teaching a friend to tread water years ago. While I feel very comfortable in the water, I found it surprisingly difficult to break down the movement. Flexible action, but no explanatory ability.

Alternatively, we might view explanation, not action, the central principle. The Feynman Technique and other tools aim at self-explanation as the final arbiter for understanding. Unfortunately, explanation isn’t a perfect proxy either, as an explanation can always be pushed deeper.

4. Understanding as Identifying Broad, Abstract Principles

For a fourth perspective, we might view understanding as seeing deeper principles, the broad patterns underlying a case, rather than its superficial details. This view is compatible with the flexible application model but seeks to define understanding in terms of a mental process rather than an outward result.

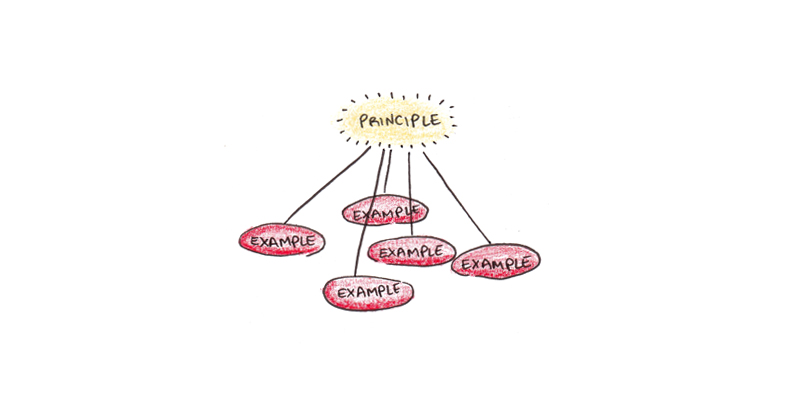
Research shows that novices tend to view physics problems in terms of superficial details (pulleys, inclined planes). In contrast, experts see the same problems in terms of principles (conservation of energy, momentum).²

There doesn’t seem to be an easy way to instill this kind of abstract appreciation in students. While pointing out principles ought to help, it may be that we need a lot of exposure to problems to view them in this way. For newbies, the abstractions are simply invisible.

5. Understanding as Concrete Mental Simulation

Instead of viewing understanding as seeing a specific problem in terms of its abstract principles, we might push in the opposite direction. Another way of understanding is the ability to visualize or simulate what is happening in a problem concretely in your mind’s eye. These kinds of mental simulations seem particularly relevant for a discipline like physics, where they played a vital role in the feats of Albert Einstein and Richard Feynman.

The idea of simulation struck me when a physics student sent me a homework problem he was struggling with. It was about electrostatic force vectors in a set of four diagrams. The task was to pick which one was different. He had wrestled with it, diagramming each charge’s contribution and adding up the component vectors.

Yet, the answer was not for calculating. Out of the four diagrams, only one wasn’t symmetrical. Symmetrical forces cancel each other. Thus, without rigorously calculating the effect, a quick mental simulation of the forces showed the answer was obviously the imbalanced picture.

In this case, “understanding” math is quite different from simply being good at calculating. In fact, it might be a different ability altogether. This understanding of the math means being able to mentally simulate the reality the equations describe and infer consequences from that simulation. This skill of “understanding” would then intertwine with calculation, but the two are of a completely different sort.

While the parallel skills of performance and understanding seem obvious in math and physics, I suspect they have analogs in most abstract domains. The ability to “see” a problem’s consequences in economics, medicine or chemistry is often a different mental operation from the symbolic activities associated with “solving” the problem.

Practical Implications of Ways of Understanding

In the case of philosophical ambiguities—such as the meaning of the words “truth,” “justice,” or “reality”—I prefer the pragmatist approach. It’s less important to define words perfectly than to be able to use them competently. As long as you and I know the difference between a truth and a falsehood, then whether or not the Correspondence Theory of Truth runs into philosophical problems isn’t relevant.

Similarly, I’m interested in the practical consequences of the understandings of understanding. What do the different theories suggest about what we ought to do to foster it?

When viewed together, some useful patterns emerge. Increased exposure to an idea or skill ought to help develop most forms of understanding. It enables us to form more connections, store more patterns, see deeper principles, and create better mental simulations. Rather than repeating the same examples, varying exposure also seems important because understanding is usually defined by dealing with novel problems rather than repeating a past solution.

However, there are differences between the models as well. If understanding depends on mental simulation, it may be a separate ability that needs practice different from symbolic approaches.

Different views of understanding, such as flexible action and explanatory ability, suggest different kinds of practice. One requires building up procedural skill through repeated use, and the other requires crafting more and more articulate theories. These ends overlap, but not entirely. There are definitely cases where you could cultivate one kind of understanding but not the other.

Ultimately, it may simply be that there’s no singular process behind understanding. Instead of seeking a single way of understanding, we must guide our practice by asking ourselves more specific questions about what we want to do with what we learn.

1. de Groot, Adriaan D.. Thought and Choice in Chess. Berlin, Boston: De Gruyter Mouton, 2014. https://doi.org/10.1515/9783110800647
2. Chi, Michelene TH, Paul J. Feltovich, and Robert Glaser. “Categorization and Representation of Physics Problems by Experts and Novices.” Cognitive Science 5, no. 2 (1981): 121-152.