Why Don’t We Use the Math We Learn in School?

How much of the math you’ve learned in school do you use in everyday life? For the majority of people, the answer is surprisingly little.

This question is at the heart of the problem of transfer of learning—how we apply what we’ve learned to new problems and situations. As readers will note, I’ve spent the better part of the last year digging into the research surrounding this topic. Why we fail to use the math we’ve learned may seem trivial, but it reveals fundamental principles of learning.

Before I get into the explanations, let’s start by examining the evidence for my assertion that most people don’t use the math they’ve learned in school.

Evidence for the Failure to Use Math

Casual observation tells us that most people don’t use math beyond simple arithmetic in everyday life. Few people make use of fractions, trigonometry, or multi-digit division algorithms they use in school. More advanced tools like algebra or calculus are even less likely to be brought out to solve everyday problems.

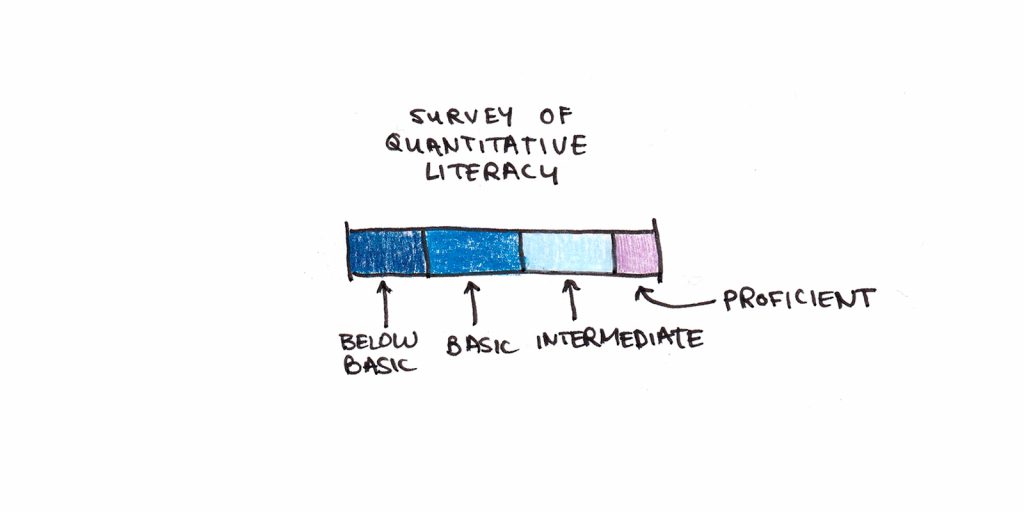
Research on the overall population’s use of math bears this out. A 2003 survey of 18,000 randomly selected Americans gave a battery of questions that embedded mathematics problems into situations they might encounter.¹ The survey authors created the following scale to rank Americans’ quantitative abilities:

• Below Basic – Add up two numbers to complete an ATM deposit.
• Basic – Calculate the cost of a sandwich and salad using prices from a menu.
• Intermediate – Calculate the total cost of ordering office supplies using a page from an office supplies catalog and an order form.
• Proficient – Calculate an employee’s share of health insurance costs for a year using a table that shows how the employee’s monthly cost varies with income and family size.

Only 13% of Americans scored as “proficient,” while over half were “basic” or “below basic.”

Anthropological studies support the observation that most people fail to use higher math. Jean Lave conducted fieldwork observing the mathematics people used in everyday life. She found that people often performed reasonably well in real-life settings, but their performance dropped when the same problems were expressed in the form of a test.²

In one frequently cited episode, an individual was trying to calculate 2/3rds of 3/4 cups of cottage cheese. Instead of applying learned math (multiplying fractions would give the easily-measurable answer of 1/2 cup), the person scooped out 2/3rds of a cup, made a rough circle on the table, and cut out a quarter.

My argument is not that nobody learns math or that math is useless. Clearly, some people learn math very well and apply it in everyday problem-solving settings. People in professions that rely on math are more likely to apply it both in and outside of work. The question is why most people don’t, in spite of spending many years practicing it.

Why Do People Fail to Use Math

I see three explanations for the failure to use math in everyday life:

1. Most people don’t learn math well enough to use it effortlessly.
2. We learn school math but fail to translate real problems into a format where we can apply our math knowledge.
3. Most higher math isn’t useful for everyday problems.

Explanation #1: Most People Don’t Learn Math Well Enough to Use It

The first argument would allege a failure of education. People don’t use math because they were never taught it thoroughly enough to use it properly.

There’s a lot in favor of this argument. One of the major barriers to using a skill in real life is automaticity. We tend to find the least-effort solution to our problem. If struggling through a math problem is hard for you, you’ll find a different way to solve it that doesn’t rely on math.

This seems the best explanation for the cottage cheese incident earlier. Suppose the person was fluent with basic fraction facts. In that case, the mental answer of “2/3 x 3/4 = 6/12 = 1/2” is much less work than scooping out cottage cheese and manipulating it manually.

A lack of automaticity may explain the difficulty people had with the quantitative questions in the survey. Their math wasn’t easily accessible, which led them to make mistakes in the reasoning tasks.

Explanation #2: Most People Don’t Know How to Translate Real-Life Situations into Math Problems

The second argument is a little different. It argues that people may develop competence in math classes, but they struggle to translate real-life problems into a format where they can use their mathematics knowledge.

This seems most apparent in the case of applying algebra. Students struggle with algebra, but they particularly struggle with word problems. Yet, the equivalent real-life problems are typically much harder than word problems.

Every word problem takes place in an algebra class, so you know that algebra will be part of the solution. Further, teachers rarely give impossible problems, so you know that your prior knowledge should be sufficient to solve it. Finally, word problems end up being stereotyped formats (trains leaving various cities) which you can use as a cue to identify which type of problem it is. Extracting an algebraic representation of real-life problem situations is typically much harder.

I can recall an example of this in our business. Where we’re located, sales tax gets added to the stated purchase price. So if we had a $10 product with 10% sales tax, you’d charge the customer $11 and set aside $1 for the government. However, our software at the time couldn’t add the sales taxes, so we had to calculate how much to send the government afterward.

Without thinking much about it, the person I was working with said we need to remit 10% of our sales. Except that isn’t right. If he had applied algebra, the problem would have been: amount collected = actual sales + actual sales * 10%. Taxes owed would then be the amount collected divided by 1.1 multiplied by 10%. For $10, that would be $0.91.

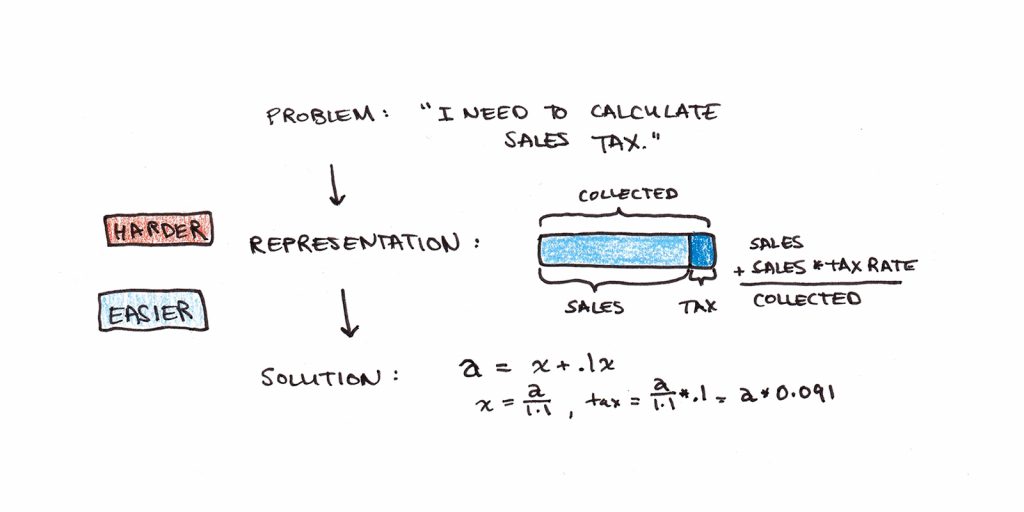
Stated as an algebra equation, the person immediately saw the correct answer. Even telling him the basic idea, that the tax amount needs to be 10% bigger than the amount leftover, got the right solution immediately. The trick was recognizing that algebra needed to be applied.

From this perspective, what people struggle with is not doing math, but recognizing where and how to apply math to real problems.

Explanation #3: Math Isn’t That Useful for Everyday Problems

A third explanation is that math is overrated as a solution strategy for problems outside of exacting, quantitative disciplines. The person measuring cottage cheese managed to get the correct answer without multiplying fractions.

There’s an interesting split in perspective on this issue when I’ve asked people about it. People who are good at math point out that it’s obviously useful and the only way to get correct answers to quantitative problems. People who are bad at math tend to discount math’s relevance to everyday life.

The math-supporters would argue that people’s failure to see the relevance of math to everyday life is due to their inability to use it. Knowledge determines what solution strategies are available to you. If knowledge is missing (as in explanation #2) or is insufficiently effortless (as in explanation #1), then you tend to view using it as expensive and unnecessary.

The math-detractors would argue that there’s a sunk-cost bias on behalf of the math experts. They’ve invested a lot of effort into learning math well. Thus, they naturally see it as the “correct” way to solve most problems, even if many problems can be solved in other ways.

Everyone values knowledge they have mastered, and tends to dismiss knowledge they haven’t as irrelevant. There’s probably bias on both sides.

I tend to lean in favor of the first group, but that might be my bias from having learned a lot of math!

How Can We Make Math More Useful?

Setting aside explanation #3 for a moment, let’s argue that the math-supporters are indeed correct about its general utility. What could we do to make math easier to apply?

There seem to be a few options:

• More drill and practice with math. More time spent drilling and practicing math makes it more available for effortless calculations. Failure to sufficiently master academic subjects results in a lot of knowledge that is inert for practical purposes.
• More practice with interpreting problem situations. Many students are only taught math as symbol manipulation. Less instruction is focused on identifying situations where it might be useful. We need to give students more training in noticing and converting everyday situations into the math problems they know how to solve.
• Give real-life challenges that require math. Ultimately, skills and knowledge are sustained by usage. If you don’t have any genuine problems that require a skill, you begin to forget it. The reason people in STEM professions maintain sharp math skills is because they need them to be sharp.

Mathematics can be a stand-in for nearly any academic subject. In all cases, to have useful skills, you need a combination of automatic skill, problem identification and interpretation, and sustaining real-world usage. Anything less and knowledge learned fails to leave the classroom.

1. Kutner, Mark, Elizabeth Greenberg, Ying Jin, Bridget Boyle, Yung-chen Hsu, and Eric Dunleavy. “Literacy in Everyday Life: Results from the 2003 National Assessment of Adult Literacy. NCES 2007-490.” National Center for Education Statistics (2007).
2. Lave, Jean. Cognition in practice: Mind, mathematics and culture in everyday life. Cambridge University Press, 1988.